从数学的角度思考,二次元的“次元”是什么?(6)
2022-10-14 来源:acgdir.com
大量可以绘制在这个平面上的图形同时也可以用方程来描述,在物理学家进一步分析运动过程中,这种“解析”方法,即“笛卡尔几何”,将成为牛顿和莱布尼茨发展微积分的基石。理解微积分的一种方法是研究曲线,这使我们能够正式标定曲线最陡峭的位置和达到局部最大或最小值的位置。被应用于运动研究中,微积分成为了一种分析和预测的方法,例如,它能分析抛向空中的物体达到最大高度需要的条件,也可以预知当球从弯曲斜坡上滚下时能保持的特定速度。微积分自出现以来就已成为几乎所有科学分支的关键工具。
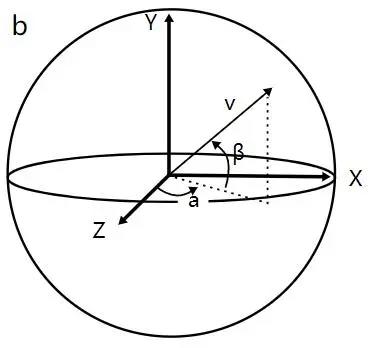
以先前的图示为例,很容易得出添加第三个轴的方式。因此,用 x、y 和 z 轴,我们可以描述出球体的表面——比如一个沙滩球的外皮。这里方程(对于半径为 1 的球体)变为:x y z = 1
通过三个轴,我们可以描述三维空间中的形状。同样,每个点都由三个坐标唯一标定:这是构造三维空间“三维性”的必要条件。
但为什么止步于此呢?如果增加上第四个维度呢?称这一维度为p。现在可以给我所谓的位于四维空间中的球体写出一个方程:x y z p = 1。我不能为你画出这个物体,但在数学上增加另一个维度是合理的,“合理”意味着这样做在逻辑上没有任何矛盾——没有理由不能这样做。
以先前的图示为例,很容易得出添加第三个轴的方式。因此,用 x、y 和 z 轴,我们可以描述出球体的表面——比如一个沙滩球的外皮。这里方程(对于半径为 1 的球体)变为:x y z = 1
通过三个轴,我们可以描述三维空间中的形状。同样,每个点都由三个坐标唯一标定:这是构造三维空间“三维性”的必要条件。
但为什么止步于此呢?如果增加上第四个维度呢?称这一维度为p。现在可以给我所谓的位于四维空间中的球体写出一个方程:x y z p = 1。我不能为你画出这个物体,但在数学上增加另一个维度是合理的,“合理”意味着这样做在逻辑上没有任何矛盾——没有理由不能这样做。
 宁次×鹿丸
宁次×鹿丸